Практично будь-що в житті можна виміряти та дослідити за допомогою графіків та точних наук. Не вірите? Професор Джордан Елленберґ, автор бестселеру «Як ніколи не помилятися», доводить, що увесь наш світ пронизаний математикою: вона демонструє його приховану красу та логіку й контролює майже всі царини нашого життя. Автор розкладає та аналізує ситуації зі світів соціології, політики, бізнесу та культури за допомогою математики і навіть пояснює, за скільки часу потрібно приїжджати в аеропорт, чим є насправді «громадська думка», чому у високих батьків низькі діти, як виграти в лотерею та безліч інших речей.

Нижче ми наводимо два уривки, якими з нами поділилося видавництво «Наш формат»: один з них демонструє, як завжди вигравати в гру на підкидання монет, а інший - чому красиві чоловіки зазвичай підлі, а популярна література - нудна і неякісна.
Про монети:
Пограймо в уявну гру. Гра зветься хто найкраще кидає монети. Вона зовсім проста. Гравці кидають жменю монет, і виграє той, у кого випадає більше гербів. Однак, щоб зробити гру трішки цікавішою, уявімо, що не в усіх гравців кількість монет однакова. Дехто — Мала команда — має лише десять монет, тоді як кожен член Великої команди має сто.
Якщо рахувати абсолютну кількість гербів, майже напевно можна сказати, що переможцем у грі буде хтось з Великої команди. Типовий гравець Великих отримає близько 50 гербів — результат, якого неможливо досягнути жодному гравцеві з Малої команди. Навіть якби у Малій команді було сто гравців, найвищими, ймовірно, будуть результати 8 або 9.
Здається, це нечесно! Велика команда має величезну закладену від початку перевагу. Тож є краща ідея. Замість того щоб рахувати абсолютні результати, будемо рахувати частки. Це має вирівняти умови для двох команд.
Але не вирівняє. Як я вже відзначав, якщо є сто «малих», принаймні в одного з них, імовірно, випаде 8 гербів. Отже, результат цього гравця буде щонайменше 80 %. А «великі»? Жоден з «великих» не отримає 80 %. Звичайно, фізично це можливо. Утім так не буде. Насправді потрібно, щоб у Великій команді було два мільярди гравців, щоб з’явився реальний шанс отримати щось схоже. Що більше монет кидаєш, то більшими є шанси наблизитися до результату 50-50.
Можете спробувати самі! Я спробував, і ось що вийшло. Кидаючи по 10 монет за раз, як гравці Малої команди, я отримав таку послідовність випадання гербів:
4, 4, 5, 6, 5, 4, 3, 3, 4, 5, 5, 9, 3, 5, 7, 4, 5, 7, 7, 9...
Зі ста монетами, як у «великих», послідовність виявилася така:
46, 54, 48, 45, 45, 52, 49, 47, 58, 40, 57, 46, 46, 51, 52, 51, 50, 60, 43, 45...
І з тисячею монет:
486, 501, 489, 472, 537, 474, 508, 510, 478, 508, 493, 511, 489, 510, 530, 490, 503, 462, 500, 494...
Гаразд, якщо чесно, то я тисячу монет не кидав. Я попросив комп’ютер змоделювати кидання. Хто має час кидати тисячу монет?
Один чоловік, Дж. Е. Керріч, мав таку нагоду. 1939 року цей південноафриканський математик необачно приїхав до Європи. Його семестр роботи за кордоном швидко обернувся на ув’язнення в таборі для інтернованих у Данії. Можливо, інший в’язень, не такий перейнятий проблемами статистики, на його місці позначав би термін рисками на стіні камери. А от Керріч кидав монету, усього 10 тисяч разів, записуючи кількість отриманих гербів. Результати виглядали десь так:
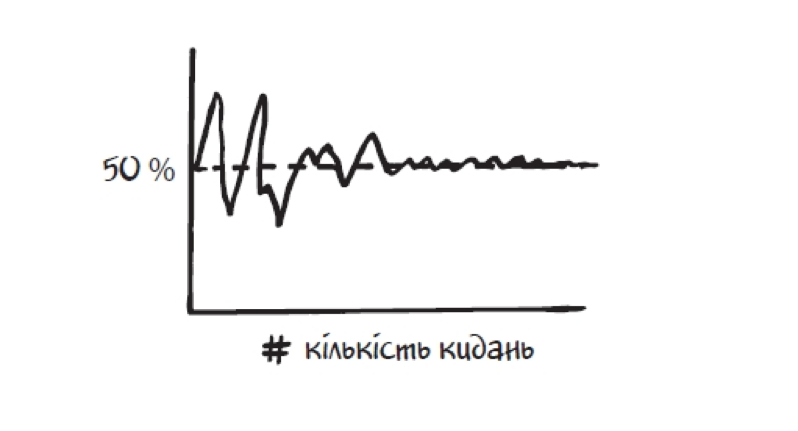
Як бачимо, частка гербів невблаганно прямує до 50 % мірою зростання кількості кидань монети — графік немовби стискується невидимими лещатами. Те саме відбувається при моделюванні. Частка гербів у першій групі кидань — Мала команда — становить від 30 до 90 %. Коли кидається сто монет за раз, діапазон звужується — лише від 40 до 60 %. А з тисячею монет діапазон часток уже становить усього від 46,2 до 53,7 %. Щось притискає результати дедалі ближче до 50 %. Це «щось» — холодна і дужа рука Закону великих чисел. Не буду наводити точного формулювання теореми (хоча воно дивовижно красиве!). По-іншому про цей закон можна сказати так: що більше монет кидається, то меншою буде ймовірність отримання 80 % гербів. Насправді за достатньо великої кількості монет надзвичайно малим стає шанс отримати навіть 51 %! В отриманні великого відхилення від 50 % при десяти киданнях немає нічого дивного; отримання такого самого перекосу на ста киданнях є таким неймовірним, що це змусить підозрювати, що щось не так з монетами.
Розуміння того, що результати експерименту тяжіють до певного середнього показника, якщо експеримент повторювати знову і знову, не нове. Воно майже так само давнє, як і саме математичне дослідження ймовірності; цей принцип неформальним чином у XVI ст. сформулював Джироламо Кардано, хоча свою яскраву назву, la loi des grands nombres, він отримав тільки на початку 1800-х, коли таким чином цей закон описав французький математик Сімеон Дені Пуассон.
Про негативну кореляцію між зовнішністю та рисами характеру:
Чи не зауважували ви, що серед усіх чоловіків (або, очевидно, «представників ґендеру, якому ви віддаєте перевагу, якщо такий є») у вашому списку можливих партнерів вродливі чоловіки зазвичай підлі, тоді як порядні зазвичай невродливі. Це тому, що симетричне обличчя робить людину жорстокою? Або тому, що гарне поводження з іншими робить тебе потворним? Ну, може й так. Але не обов’язково. Нижче я подаю Великий квадрат чоловіків:
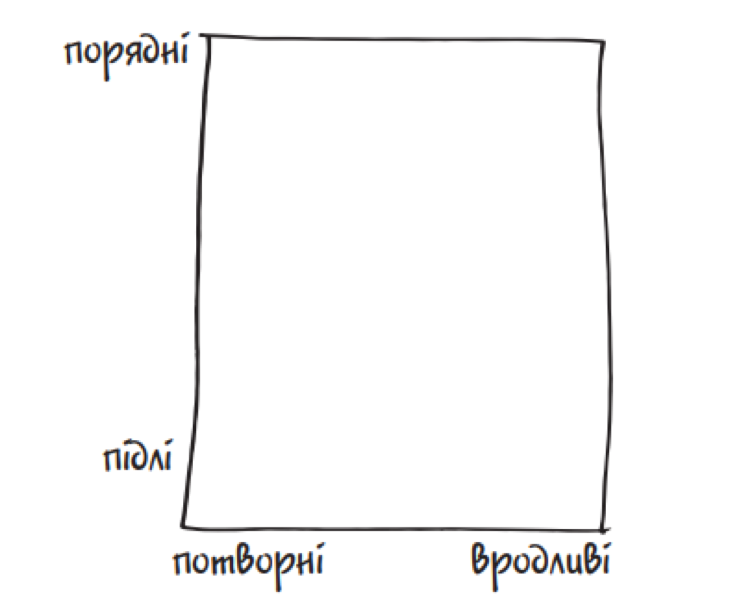
і в рамках робочої гіпотези припускаю, що всі чоловіки рівномірно розподілені по цьому квадрату. Зокрема, тут приблизно в рівній кількості є порядні вродливі, порядні потворні, підлі вродливі й підлі потворні чоловіки. Однак у хорошого характеру і привабливої зовнішності є спільний ефект: вони поміщають чоловіків до тієї групи, на яку ви звертаєте увагу. Будемо чесними: підлі виродки — це ж ті, кого ви не розглядаєте. Таким чином, усередині Великого квадрата є Малий трикутник прийнятних чоловіків:
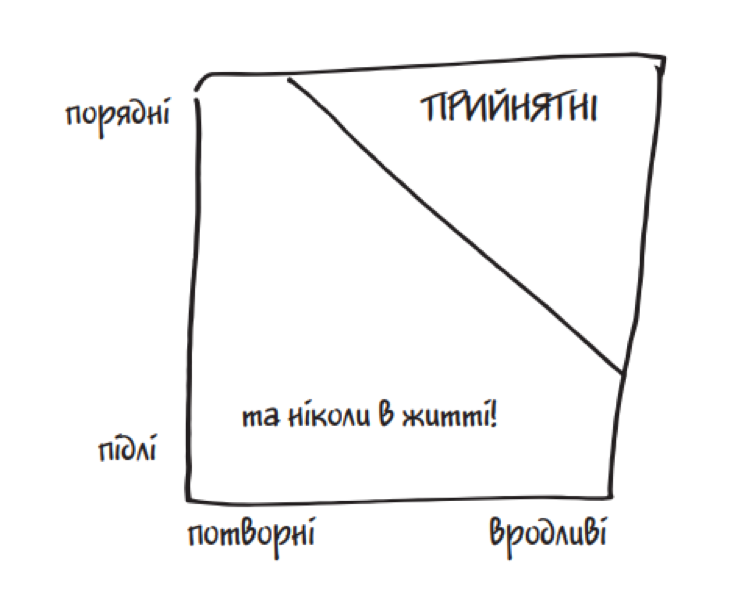
Тепер усе ясно. Найкрасивіші чоловіки у вашому трикутнику представляють увесь діапазон особистостей, від найпорядніших до найпідліших. У середньому вони майже так само вродливі, як середньостатистичний чоловік серед усього населення, яке, мусимо визнати, не надто привабливе. Своєю чергою, найпорядніші чоловіки лише в середньому вродливі.
Однак некрасиві хлопці, які вам подобаються — вони утворюють крихітний кутик трикутника, — дуже порядні люди, і вони мусять такими бути, інакше ви їх узагалі не помітите.
Негативна кореляція між зовнішністю і особистими якостями серед ваших потенційних обранців абсолютно реальна. Однак якщо ви спробуєте поліп- шити фігуру свого хлопця, навчивши його підлої поведінки, ви станете жертвою помилки Берксона.
Те саме з літературним снобізмом. Ви знаєте, чому популярні романи такі жахливі? Річ не в тім, що маси не цінують якість. Просто є Великий квадрат романів, і єдині романи, про які ви хоч колись чули, — це ті, що в Трикутнику прийнятних романів, — вони або популярні, або хороші.
